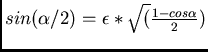
Some usefull trigonometry stuff:

Functions of half of the angle:

$sin(\alpha /2) = \epsilon * \sqrt(\frac{1-cos\alpha}{2})$

$tg(\alpha /2) = \nu * \sqrt(\frac{1-cos\alpha}{1+cos\alpha}) = = \frac{1-cos\alpha}{sin\alpha} = \frac{sin\alpha}{1+cos\alpha}$

$cos(\alpha /2) = \eta * \sqrt(\frac{1+cos\alpha}{2})$

$ctg(\alpha /2) = \nu * \sqrt(\frac{1+cos\alpha}{1-cos\alpha}) = = \frac{1+cos\alpha}{sin\alpha} = \frac{sin\alpha}{1-cos\alpha}$

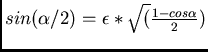
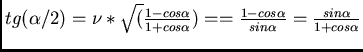
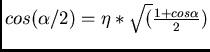
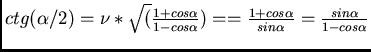
where: $\epsilon = sign(sin\frac{\alpha}{2})$,

$\eta=sign(cos\frac{\alpha}{2})$,

$\nu=sign(tg\frac{\alpha}{2})$,

Sum of functions:

$sin\alpha + sin\beta = 2\cdot sin\frac{\alpha+\beta}{2} \cdot cos\frac{\alpha-\beta}{2}$

$sin\alpha - sin\beta = 2\cdot cos\frac{\alpha+\beta}{2} \cdot sin\frac{\alpha-\beta}{2}$

$cos\alpha + cos\beta = 2\cdot cos\frac{\alpha+\beta}{2} \cdot cos\frac{\alpha-\beta}{2}$

$cos\alpha - cos\beta = -2\cdot sin\frac{\alpha+\beta}{2} \cdot sin\frac{\alpha-\beta}{2}$

$1+cos\alpha = 2\cdot cos^2\frac{\alpha}{2}$

$1-cos\alpha = 2\cdot sin^2\frac{\alpha}{2}$

$tg\alpha + ctg\beta = \frac{cos(\alpha - \beta)}{cos\alpha sin\beta}$

Multiplication of functions:

$sin\alpha \cdot sin\beta = \frac{1}{2}[cos(\alpha-\beta)-cos(\alpha+\beta)]$

$cos\alpha \cdot cos\beta = \frac{1}{2}[cos(\alpha-\beta)+cos(\alpha+\beta)]$

$sin\alpha \cdot cos\beta = \frac{1}{2}[sin(\alpha-\beta)+sin(\alpha+\beta)]$

Power of functions:

$sin^2\alpha = \frac{1}{2}\cdot (1-cos2\alpha)$

Functions of doubled angle:

$sin2\alpha = 2sin\alpha \cdot cos\alpha$

$cos2\alpha = cos^2\alpha - sin^2\alpha = 2cos^2\alpha -1 = 1 - 2sin^2\alpha$

$tg2\alpha = \frac{2tag\alpha}{1-tg^2\alpha}$

$ctg2\alpha = \frac{ctg^2\alpha -1}{2ctg\alpha}$