Czastka przechodzaca przez materie

Zalozmy ze mamy czastke o masie M i predkosci $\overline{v}$, ktora oddzialywuje z osrodkiem detektora poprzez foton o energii $h\omega$ i pedzie $h\overline k$ (patrz rysunek)

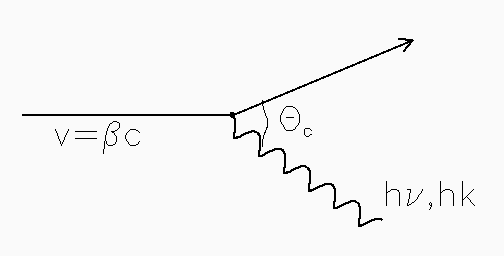
Zachowanie energii i pedu moze byc zapisane tak:

(1) $h\omega (1 - h\omega /2\gamma Mc^2 ) = h \overline k \cdot \overline v - h \cdot k^2 /2\gamma M$

Jesli nalozymy warunek na miekkosc oddzialywania: $h\omega \le \gamma Mc^2$ oraz: $hk \le v\gamma M$ to powyzsze rownanie redukuje sie do:

(2) $\omega = \overline v \cdot \overline k$

Zachowanie fotonu w medium jest opisywane relacja dyspersji:

(3) $\omega^2 - k^2 c^2/\epsilon = 0$

gdzie $\epsilon$ to stala dielektryczna. Z rownan (2) i (3), eliminujac $\omega$ i $k$, otrzymujemy:

(4) $\sqrt{\epsilon} v/c \cdot cos\Theta_c =1$

gdzie $\Theta_c$ to kat pomiedzy $\overline v$ i $\overline k$ (patrz rysunek). Z tego mozna zauwazyc ze jesli $v/c \cdot \sqrt{\epsilon}$ jest wieksze niz 1 to istnieje rzeczywisty kat $\Theta_c$ w ktory moga byc emitowane rzeczywiste fotony. Zjawisko to nazywamy promieniowaniem Cerenkova, $\Theta_c$ to kat Cerenkova a $v=c/\sqrt{\epsilon}$ to prog Cerenkova, ponizej ktorego $cos\Theta_c$ jest wieksza niz 1 i rzeczywiste fotony nie sa emitowane (przynajmniej w jednorodnym osrodku)

Jak dotad zakladalismy ze $\epsilon$ jest rzeczywiste, co jest prawda tylko ponizej progu jonizacji. Mozemy wyroznic trzy regiony o innej fenomenologii w zaleznosci od $\epsilon$ i $v$:

• Region optyczny gdzie $\epsilon$ jest rzeczywiste i wieksze od 1, osrodek jest przezroczysty dla emitowanych fotonow. Fotony emitowane sa dzieki mechanizmowi Cerenkova oraz dzieki optycznemu promieniowaniu przejscia, ktore jest promieniowaniem Cerenkova emitowanym na niejednorodnosciach osrodka.
• Region absorpcyjny gdzie $\epsilon$ jest zespolone i zasieg fotonow jest maly - sa one absorbowane przez material i daja przyczynek do jonizacji osrodka. Ten region jest glownie odpowiedzialny za efekt $dE/dx$.
• Region rentgenowski gdzie $\epsilon$ jest mniejsze niz 1 i prog Cerenkova jest wiekszy niz $c$. Promieniowanie Cerenkova na niejednorodnosciach osrodka zwane promieniowaniem przejscia jest emitowane tym razem w zakresie rentgenowskim, dajac podstawy do dzialania detektorow promieniowania przejscia.